842
842
如图,一只蚂蚁从单位正方体
- 分别写出
的值; - 设顶点
出发经过 步到达点 的概率为 , 求 的值. - 求
.
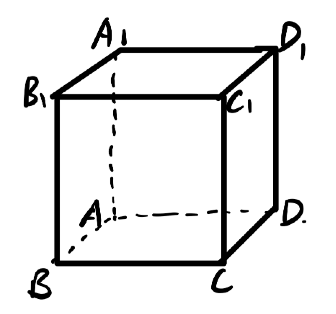
解 钱莘芪
出发一步不可能回到 ; 出发两步再回到 必须在第二步沿原路折返,这样 . - 根据对称性,从
出发经过 步到达 是等可能的. 每经过一步,蚂蚁所在的点都会在两个集合 间切换,因此 - 要使
出发经过 步到达 , 或者要求出发 步后在 ,并再走两步回到 ,或者要求 步后在 , 并再走两步回到 , 这样 而由2得 消去 得
分别对奇偶数递推得