879
879
在平面直角坐标系
- 若点
的横坐标为 ,求 的长; - 设
的上、下顶点分别为 , 记 的面积为 , 的面积为 , 若 , 求 的取值范围; - 若点
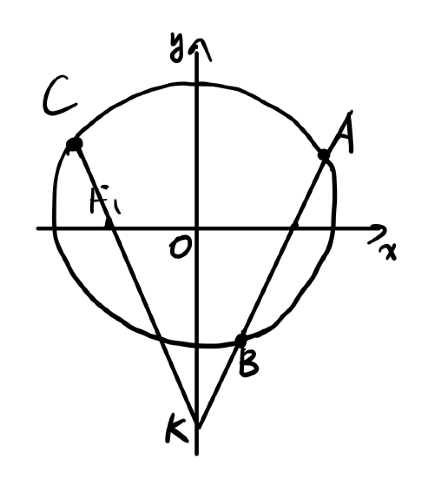
在 轴上方,设直线 与 交于点 , 与 轴交于点 , 延长线与 交于点 , 是否存在 轴上方的点 ,使得 成立? 若存在,请求出点 的坐标; 若不存在,请说明理由.
解 钱莘芪
- 在
的方程中代入 得 , 进而 . . 两边平方得
(我们不承认三点共线的退化三角形,因此令). 进而 - 结合题目描述做出图形. 这样可以注意到
关于 轴对称. 记 则 . 而 ,因此 . 根据条件这两个向量平行,因此
这样, 因此
另一方面由, 作差得
解得, 故 存在且坐标为 .